Random-effects meta-analysis typically assumes a normal distribution for the study-specific effects allowing for some variability across studies. However, the extend of acceptable heterogeneity and its impact on conclusions remain unclear. When meta-regression with study-level covariates fails to explain the variability among studies, residual heterogeneity may remain, leading to unknown distributions for the random effects. Moreover, in presence of outliers, asymmetric distributions might describe the structure of the data better than the normal distribution. In such cases, the estimated mean of the random-effects distribution may no longer represent a meaningful summary of the studies at hand. Alternative options have been suggested but rarely used in published meta-analyses. This thesis aims to deal with models that relax the random-effects normality assumption through three different projects.
The first project aimed to conduct a methodological systematic review to identify meta-analysis models assuming non-normal distributions for the random effects. Eligible articles included new meta-analysis models, simulation studies or commentaries on model properties. A total of 27 articles describing 24 parametric or semi-parametric models were identified through PubMed and other related journals.
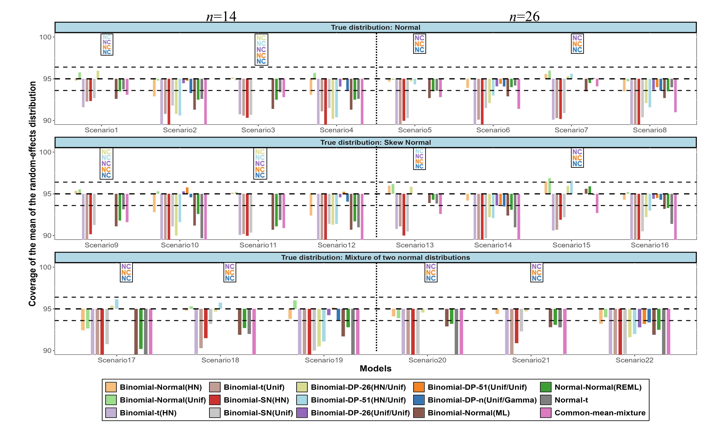
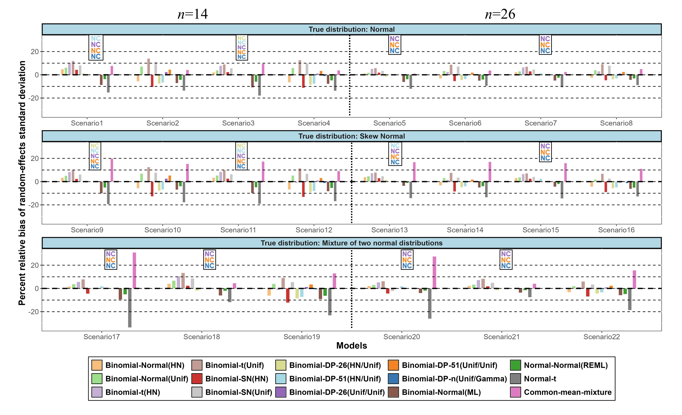
These models fall into four categories: heavy-tailed and skewed distributions, beta distributions, mixtures of distributions, and Dirichlet process (DP) priors. The proposed models have been evaluated through small simulation studies or illustrative examples with authors often claiming the superiority of their methods over the standard normal model, under certain conditions. The second project investigated the performance of several flexible random-effects models under an extensive simulation study. Fifteen models, including the normal, implemented in the Frequentist or Bayesian framework, were compared in terms of various measures such as bias and coverage probability. Twenty-two scenarios were considered varying the true mean and variance of the random-effects distribution, the number of included studies, and the shape of the true distribution. Results revealed small differences in bias between the different models but larger differences in coverage probabilities and precision. In scenarios with large random-effects variance, all models were substantially biased in estimating the mean of the random-effects distribution. DP models in some scenarios revealed latent underlying clustering of studies.
These findings imply that when substantial heterogeneity is suspected focusing only on the mean of the random-effects distribution could be misleading, as it can be inaccurately estimated. Hence, researchers could start with the normal model and consider alternative models as sensitivity analysis in view of seemingly non-normal data. The third project further explores the real impact of adding flexibility to the random-effects distribution on meta-analytic results. A meta-analysis of 58 cohort studies comparing the cognitive functioning between preterm- and term-born children was used. Despite the presence of heterogeneity, subgroup and meta-regression analyses, failed in identifying its sources. The results between 8 random-effects models were compared, showing minor differences in the estimated mean of the random-effects distribution but larger discrepancies for the random-effects variance. Skewed and t-distribution models exhibited negatively skewed and highly peaked posterior random-effects distributions. The DP model revealed the presence of clusters of studies suggesting that the observed heterogeneity may be explained by a combination of particular study-level characteristics. While flexible random-effects models, might not affect materially the summary estimates, they may help to explain residual heterogeneity and provide better insights into the underlying-effects distribution and interpretation of the findings.
- https://link.springer.com/article/10.1186/s12874-025-02658-3?utm_source=rct_congratemailt&utm_medium=email&utm_campaign=oa_20251016&utm_content=10.1186%2Fs12874-025-02658-3
Keywords: evidence synthesis, random-effects meta-analysis, heterogeneity, non-normal data, skewed-data, outliers, flexible parametric models, semi-parametric models
By Kanella Panagiotopoulou
kanellapanag@gmail.com