Modélisation des écarts à la normalité dans la méta-analyse
La méta-analyse à effets aléatoires suppose généralement une distribution normale des effets spécifiques aux études, permettant une certaine variabilité entre les études. Cependant, le niveau d’hétérogénéité acceptable et son impact sur les conclusions restent incertains. Lorsque la méta-régression échoue à expliquer la variabilité parmi les études, une hétérogénéité résiduelle peut subsister, conduisant à des distributions inconnues pour les effets aléatoires. De plus, en présence des études aberrantes, des distributions asymétriques peuvent mieux modéliser la structure des données que la distribution normale. Dans de tels cas, la moyenne de la distribution des effets aléatoires peut ne plus représenter un résumé pertinent des études incluses. Des modèles alternatifs ont été proposés, mais demeurent rarement utilisés dans les méta-analyses publiées. Cette thèse propose d’étudier les modèles qui assouplissent l’hypothèse de normalité des effets aléatoires à travers trois projets distincts. Le premier projet visait à mener une revue méthodologique systématique afin d’identifier les modèles de méta-analyse supposant des distributions non normales des effets aléatoires.
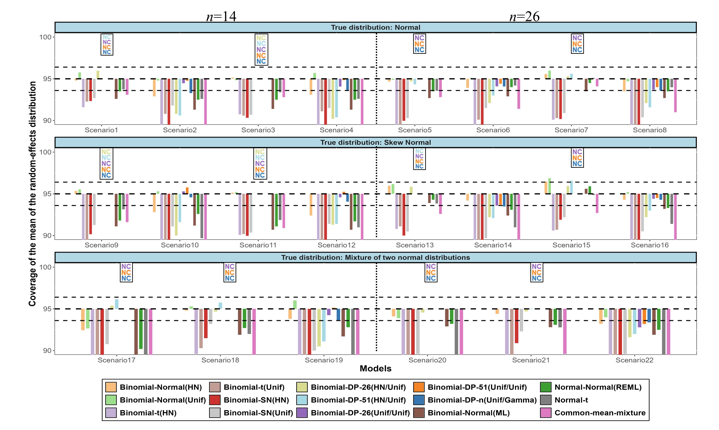
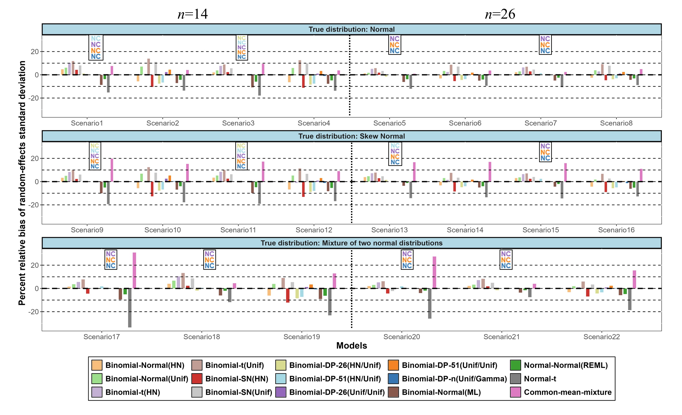
Un total de 27 articles décrivant 24 modèles paramétriques ou semi-paramétriques ont été identifiés via PubMed et d’autres revues connexes, réparties en quatre catégories : distributions à queues lourdes et asymétriques, distributions bêta, mélanges de distributions, et distributions avec un a priori de processus de Dirichlet (DP). Le deuxième projet a étudié la performance de plusieurs modèles flexibles à effets aléatoires dans le cadre d’une étude de simulation approfondie. Quinze modèles, dont le modèle normal, implémentés dans un cadre fréquentiste ou bayésien, ont été comparés selon différentes mesures de performance. Vingt-deux scénarios ont été considérés en faisant varier la moyenne et la variance réelle de la distribution des effets aléatoires, le nombre d’études et la forme de la distribution réelle.
Les résultats ont révélé de faibles différences de biais entre les différents modèles, mais des différences plus marquées dans les probabilités de couverture. Dans les scénarios avec une grande variance des effets aléatoires, tous les modèles étaient fortement biaisés dans l’estimation de la moyenne de la distribution des effets aléatoires. Dans certains scénarios, les modèles DP ont révélé des regroupements latents des études. Ainsi, lorsqu’une hétérogénéité importante est suspectée, se focaliser uniquement sur la moyenne de la distribution des effets aléatoires pourrait induire en erreur, car elle peut être mal estimée. Les chercheurs pourraient commencer par le modèle normal, puis considérer d’autres alternatives dans une analyse de sensibilité lorsque les données semblent s’écarter de la normalité.
Le troisième projet a exploré l’impact de l’utilisation de modèles à effets aléatoires plus flexibles à partir d’une méta-analyse de 58 études de cohorte comparant le fonctionnement cognitif des enfants nés prématurément et à terme. Malgré la présence d’hétérogénéité, les analyses de sous-groupes et de méta-régression n’ont pas permis d’en identifier les sources. Les résultats de huit modèles à effets aléatoires ont été comparés, montrant de faibles différences dans la moyenne estimée de la distribution des effets aléatoires, mais des écarts plus marqués pour la variance des effets aléatoires.
Les modèles à distribution asymétrique ont produit des distributions a posteriori des effets aléatoires asymétriques et présentant des pics prononcés. Le modèle DP a révélé la présence de groupes suggérant que l’hétérogénéité observée pourrait s’expliquer par une combinaison particulière des caractéristiques des études. Bien que les modèles flexibles ne puissent pas affecter de manière significative les estimations globales, ils aident à expliquer l’hétérogénéité résiduelle et fournir des éclairages plus précis sur la distribution des effets sous-jacents.
Mots-clef : synthèse des données probantes, méta-analyse à effets aléatoires, hétérogénéité, données non normales, données asymétriques, valeurs aberrantes, modèles paramétriques flexibles, modèles semi-paramétriques
Par Kanella Panagiotopoulou
Crédits photo : Kanella Panagiotopoulou